Python 位运算符、位运算高级运用

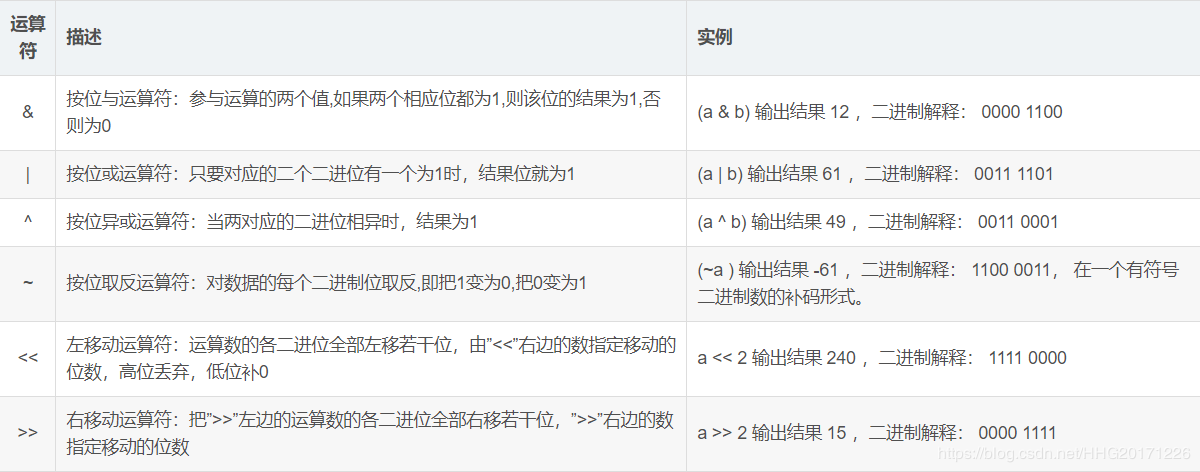
按位运算符是把数字看作二进制来进行计算的。Python中的按位运算法则如下： 下表中变量 a 为 60，b 为 13，二进制格式如下：

a = 0011 1100

b = 0000 1101

-----------------

a&b = 0000 1100

a|b = 0011 1101

a^b = 0011 0001

~a  = 1100 0011

位运算高级运用

1. 判断奇偶数

如果把 n 以二进制的形式展示的话，其实我们只需要判断最后一个二进制位是 1 还是 0 就行了，如果是 1 的话，代表是奇数，如果是 0 则代表是偶数，所以采用位运算的方式的话，代码如下：

if(n & 1 == 1){
    // n 是个奇数。
}

2、交换两个数

交换两个数相信很多人天天写过，我也相信你每次都会使用一个额外来变量来辅助交换，例如，我们要交换 x 与 y 值，传统代码如下：

int tmp = x;
x = y;
y = tmp;

万一哪天有人要为难你，不允许你使用额外的辅助变量来完成交换呢？你还别说，有人面试确实被问过，这个时候，位运算大法就来了。代码如下：

x = x ^ y   // （1）
y = x ^ y   // （2）
x = x ^ y   // （3）

两个相同的数异或之后结果会等于 0，即n ^ n = 0。并且任何数与 0 异或等于它本身，即 n ^ 0 = n。

把（1）中的 x 带入 （2）中的 x，有

y = x ^ y = (x ^ y) ^ y = x ^ (y ^ y) = x^0 = x。 x 的值成功赋给了 y。

对于（3）,推导如下：

x = x ^ y = (x ^ y) ^ x = (x ^ x) ^ y = 0^y = y。

异或运算支持运算的交换律和结合律

3、找出没有重复的数

给你一组整型数据，这些数据中，其中有一个数只出现了一次，其他的数都出现了两次，让你来找出一个数 。

例如这组数据是：1， 2， 3， 4， 5， 1， 2， 3， 4。其中 5 只出现了一次，其他都出现了两次，把他们全部异或一下，结果如下：

由于异或支持交换律和结合律，所以:

1 ^ 2 ^ 3 ^ 4 ^ 5 ^ 1 ^ 2 ^ 3 ^ 4 = （1 ^ 1) ^ ( 2 ^ 2 ) ^ (3^ 3) ^ (4 ^ 4) ^ 5= 0 ^ 0 ^ 0 ^0 ^5 = 5。

def singleNumber3( nums):
    """
    :type nums: List[int]
    :rtype: int
    """
    a = 0
    for i in nums:
        a ^= i
    return a

4、m的n次方

如果让你求解 m 的 n 次方，并且不能使用系统自带的 pow 函数，你会怎么做呢？这还不简单，连续让 n 个 m 相乘就行了，代码如下：

int pow(int n){
    int tmp = 1;
    for(int i = 1; i <= n; i++) {
        tmp = tmp * m;
    }
    return tmp;
}

我举个例子吧，例如 n = 13，则 n 的二进制表示为 1101, 那么 m 的 13 次方可以拆解为:

m ^ 1101 = m^0001 m^0100 m^1000。

我们可以通过 & 1和 >>1 来逐位读取 1101，为1时将该位代表的乘数累乘到最终结果。直接看代码吧，反而容易理解：

int pow(int n){
    int sum = 1;
    int tmp = m;
    while(n != 0){
        if(n & 1 == 1){
            sum *= tmp;
        }
        tmp *= tmp;
        n = n >> 1;
    }

    return sum;
}

5、找出不大于N的最大的2的幂指数

传统的做法就是让 1 不断着乘以 2，代码如下：

int findN(int N){
    int sum = 1;
   while(true){
        if(sum * 2 > N){
            return sum;
        }
        sum = sum * 2;
   }
}

例如 N = 19，那么转换成二进制就是 00010011（这里为了方便，我采用8位的二进制来表示）。那么我们要找的数就是，把二进制中最左边的 1 保留，后面的 1 全部变为 0。即我们的目标数是 00010000。那么如何获得这个数呢？相应解法如下： 1、找到最左边的 1，然后把它右边的所有 0 变成 1

2、把得到的数值加 1，可以得到 00100000即 00011111 + 1 = 00100000。 3、把 得到的 00100000 向右移动一位，即可得到 00010000，即 00100000 >> 1 = 00010000。

那么问题来了，第一步中把最左边 1 中后面的 0 转化为 1 该怎么弄呢？我先给出代码再解释吧。下面这段代码就可以把最左边 1 中后面的 0 全部转化为 1，

n |= n >> 1;
n |= n >> 2;
n |= n >> 4;

就是通过把 n 右移并且做或运算即可得到。我们假设最左边的 1 处于二进制位中的第 k 位(从左往右数),那么把 n 右移一位之后，那么得到的结果中第 k+1 位也必定为 1,然后把 n 与右移后的结果做或运算，那么得到的结果中第 k 和 第 k + 1 位必定是 1;同样的道理，再次把 n 右移两位，那么得到的结果中第 k+2和第 k+3 位必定是 1,然后再次做或运算，那么就能得到第 k, k+1, k+2, k+3 都是 1，如此往复下去…. 最终的代码如下

int findN(int n){
    n |= n >> 1;
    n |= n >> 2;
    n |= n >> 4;
    n |= n >> 8 // 整型一般是 32 位，上面我是假设 8 位。
    return (n + 1) >> 1;
}